参数估计与假设检验

# 点估计

设总体 $X$ 的分布函数形式已知，但它的一个或多个参数未知，借助于总体 $X$ 的一个样本来估计总体未知参数的值的问题称为参数的点估计问题。

# 矩估计法

样本矩

$$A_l = \frac{1}{n}\sum_{i = 1}^n X_i^l, l = 1,2,\cdots, k.$$

总体矩

$$\mu_l = E(X^l) = \begin{cases} \int_{-\infty}^{\infty}x^l f(x;\theta_1, \theta_2, \cdots, \theta_k)\text{d}x & X \text{为连续型，} \\ \sum x^l p(x;\theta_1, \theta_2, \cdots, \theta_k) & X\text{为离散型.} \end{cases}$$

可以用样本矩作为相应的总体矩的估计量。设（有多少个需要估计的参数就列多少个方程）

$$\begin{cases} \mu_1 = E(X) = \mu_1(\theta_1, \theta_2, \cdots, \theta_k),\\ \mu_2 = E(X^2) = D(X) + [E(X)]^2 = \mu_2(\theta_1, \theta_2, \cdots, \theta_k)\\ \cdots\ \cdots\ \cdots \\ \mu_k = \mu_k(\theta_1, \theta_2, \cdots, \theta_k) \end{cases}$$

由上述方程组解出 $\theta_1, \theta_2, \cdots, \theta_k$ （用 $\mu_1, \mu_2, \cdots, \mu_k$ 表示），然后用 $A_1, A_2, \cdots, A_k$ 替换 $\mu_1, \mu_2, \cdots, \mu_k$ 即得总体分布中未知参数的矩估计量。

# 最大似然估计

若总体 $X$ 为离散型， $X_1, X_2, \cdots, X_n$ 是来自 $X$ 的样本，对应的观察值为 $x_1, x_2, \cdots, x_n$ ，则这组样本取到这组对应观察值的概率为

$$L(\theta) = L(x_1, x_2, \cdots, x_n; \theta) = \prod_{i = 1}^n p(x_i; \theta)$$

其中， $\theta$ 是总体 $X$ 的参数， $p(x_i; \theta)$ 是 $X$ 的概率密度函数， $L(\theta)$ 称为样本的似然函数， $\theta$ 是未知参数。一个直观的想法是，我们已经观察到样本取到 $x_1, x_2, \cdots, x_n$ 这组观察值，那么使这组观察值出现的概率最大的 $\theta$ 就是我们要求的参数估计，记为 $\hat{\theta}$ 。这种方法称为最大似然估计法。

若总体 $X$ 为连续型，似然函数变为

$$L(\theta) = L(x_1, x_2, \cdots, x_n; \theta) = \prod_{i = 1}^n f(x_i; \theta)$$

两者都只要从方程

$$\frac{\text{d}}{\text{d}\theta}\ln L(\theta) = 0$$

中解出 $\theta$ 即可。

# 估计量的标准

1. 无偏性： $\mathbb{E}(\hat{\theta}) = \theta$ ，即估计量的数学期望等于真实参数值。PS：任意阶样本矩都是总体矩的无偏估计量。
2. 有效性： 对 $\theta$ 的两个无偏估计量 $\hat{\theta}_1, \hat{\theta}_2$ ，若 $D(\hat{\theta}_1) \leq D(\hat{\theta}_2)$ ，则称 $\hat{\theta}_1$ 更有效。
3. 相合性： 若 $\theta$ 的估计量 $\hat{\theta}$ 当样本容量 $n\rightarrow \infty$ 时收敛于 $\theta$ ，则称 $\hat{\theta}$ 为 $\theta$ 的相合估计量。

# 区间估计

对于给定的显著性水平 $\alpha\, (0 < \alpha < 1)$ ，若由来自样本 $X_1, X_2, \cdots, X_n$ 确定的统计量 $\theta_1, \theta_2$ ，使得

$$P(\theta_1 < \theta < \theta_2) = 1 - \alpha$$

则称 $(\theta_1, \theta_2)$ 为总体参数 $\theta$ 的 置信水平为 $1 - \alpha$ 的置信区间， $1 - \alpha$ 为置信水平。其核心思想是多次抽样得到的多个区间中，包含总体参数 $\theta$ 真值的区间数量占总区间数量的比例为 $1 - \alpha$ ，或每次抽样得到的区间包含 $\theta$ 真值的概率为 $1 - \alpha$ 。

补充：二项分布 $B(n, p)$ 总体对 $p$ 的区间估计为 $\left(\hat{p} \pm Z_{\frac{\alpha}{2}}\sqrt{\frac{\hat{p}(1 - \hat{p})}{n}}\right)$ 。

# 假设检验

基本思想：对总体的参数作出假设，然后通过抽样进行统计分析，从而判断假设是否成立。弃真错误的概率为 $\alpha$ 。

提出无效假设 / 反假设（Null Hypothesis, $H_0$ ）和备择假设（Alternative Hypothesis, $H_1$ ），单边（ $\theta = \theta_0$ ）还是双边（ $\theta < \theta_0$ 或 $\theta > \theta_0$ ），选定显著性水平 $\alpha$ 。

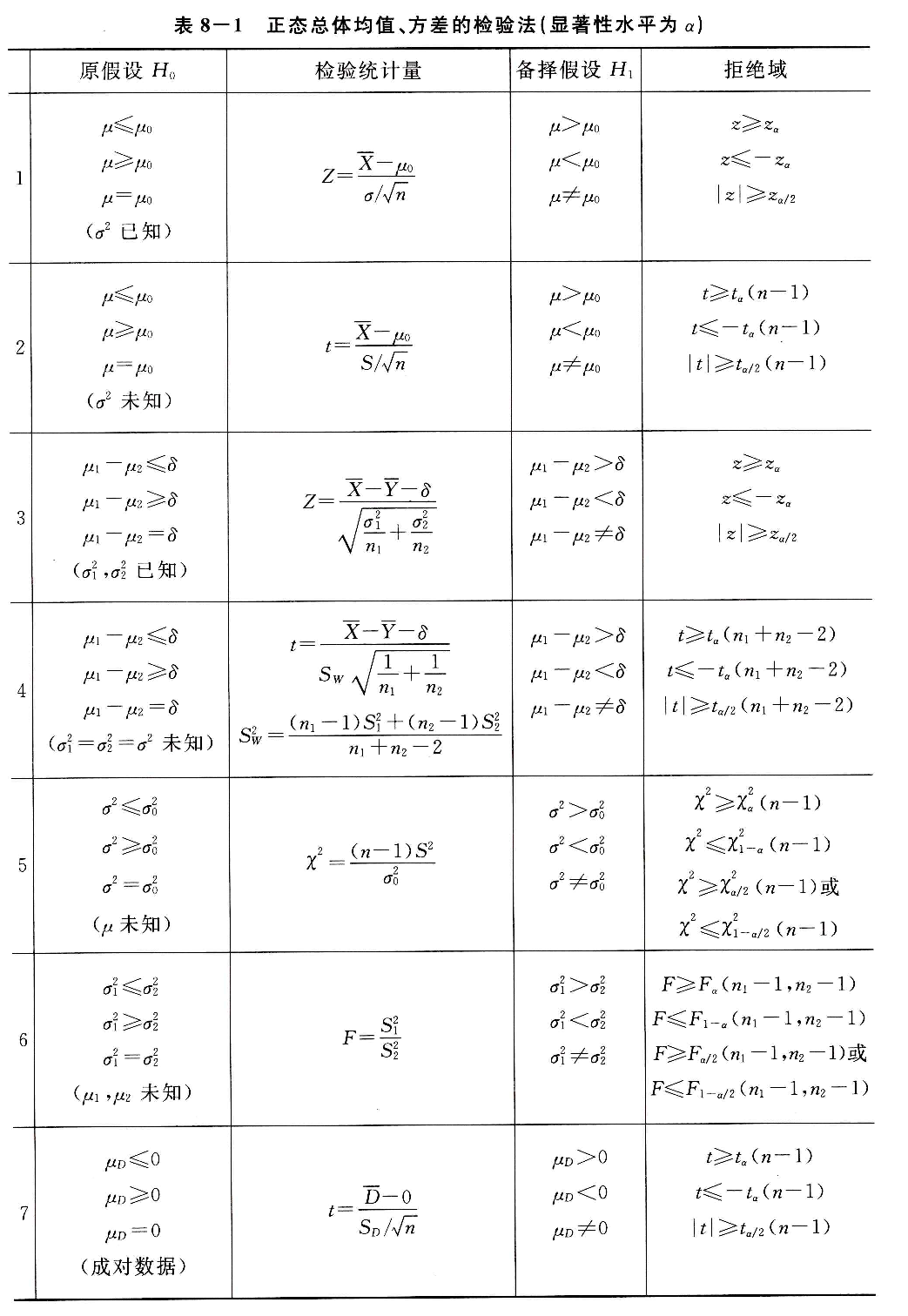
# 正态总体

# 二项总体

1. 单个总体检验：

   检验统计量 $Z = \frac{\hat{p} - p_0}{\sqrt{\frac{\hat{p}(1 - \hat{p})}{n}}}$ ， $p_0$ 为假设的总体比例， $n$ 为样本容量， $\hat{p}$ 为样本比例。

检验统计量 $Z = \frac{\hat{p}_1 - \hat{p}_2}{\sqrt{\hat{p}(1-\hat{p})\left(\frac{1}{n_1} + \frac{1}{n_2}\right)}}$ ，其中 $\hat{p} = \frac{x_1 + x_2}{n_1 + n_2}$ ，$x_1,x_2$ 为关注样本的频数， $\hat{p}_1, \hat{p}_2$ 分别为两个样本比例， $n_1, n_2$ 分别为两个样本容量。

# 卡方列联表

$$\chi^2 = \sum_{i = 1}^{r}\sum_{j = 1}^{c}\frac{(n_{ij} - \frac{n_{i\cdot} n_{\cdot j}}{n})}{\frac{n_{i\cdot} n_{\cdot j}}{n}}$$

其中 $r, c$ 分别为行数和列数。当 $\chi^2 \geq \chi_\alpha^2((r - 1)(c - 1))$ 时，拒绝 $H_0$ ，否则接受 $H_0$ 。

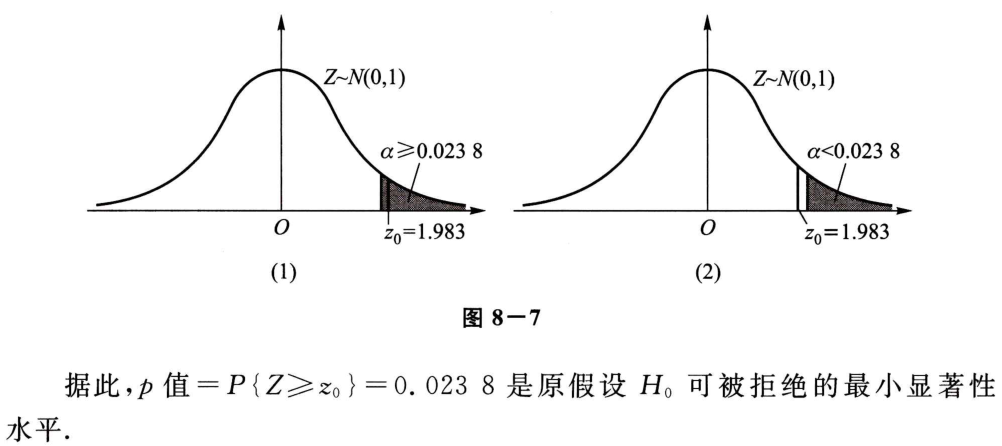
# $p$ 值法

假设检验问题的 $p$ 值是由检验统计量的样本观察值得出的原假设可被拒绝的最小显著性水平。若 $p \leq \alpha$ ，则拒绝 $H_0$ ，否则接受 $H_0$ 。

看一个例子：

参考资料：《概率论与数理统计》第五版 (盛骤等)，高等教育出版社